|
Fórmulas - |
|
La matemática podría definirse como el arte de escoger la notación adecuada. Y como casi siempre que la funcionalidad se alcanza con brillantez la belleza acaba apareciendo. La quinta esencia de lo que acabo de decir reside en las fórmulas. |
|||||
Índice
|
|||||
 |
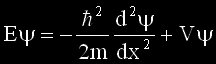La fórmulita de la izquierda es la ecuación de ondas de Schrödinger para una partícula de energía total E, moviéndose en una dimensión x, en una región de potencial V, siendo m la masa de la partícula y ψ la amplitud de probabilidad. La ecuación de ondas describe la probabilidad de que un electrón esté en una determinada posición. Como ocurre con otras muchas ecuaciones diferenciales, no se puede resolver de modo exacto salvo en determinadas situaciones (el propio Schrödinger la resolvió para el átomo de hidrógeno). Sin embargo, sí que puede ser resuelta con gran precisión mediante apróximaciones numéricas. Lo asombroso es que funciona. Bibliografía: |
 |
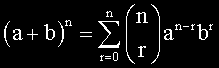En notación moderna esta es la forma que toma el teorema binomial para n natural. Descubierto en China en el siglo XII, sería conocido en Europa a mediados del siglo XVII gracias a un trabajo póstumo de Pascal. Newton lo generalizaría para exponentes negativos y fraccionarios (mediante series infinitas), razón esta por la que se le asocia el nombre de Newton. Leibniz, que nunca está lejos, fue más allá generalizando el teorema binomial en el multinomial. No solo a mí me parece bonito: también a Pessoa. Una forma de evitar tener que calcular uno a uno todos los coeficientes es utilizar el mal llamado Triángulo de Pascal, pues los coeficientes de la potencia n aparecen en la fila n+1 de dicho triángulo. Un ejemplo: aplicando la fórmula y la definición de número combinatorio tendríamos: (a + b)3 = 1·a3 + 3·a2b + 3·ab2 + 1·b3. Pero hubiese sido más rápido ir a la fila 3 + 1 del triángulo de Pascal y ver que los números que aparecen son, precisamente, los coeficientes 1, 3, 3 y 1. |
 |
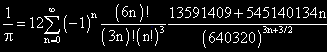Los hermanos Chudnovsky son famosos por haber desarrollado algoritmos que les han permitido calcular miles de millones de decimales del número π. Kike (7-3-2005) manda esta fórmula desarrollada por ellos y dice: "Es del estilo de la de Ramanujan, pero si la de él en cada paso sacaba 7 decimales exactos de Pi, con esta sacamos 14". Yo no la he probado, pero la he encontrado en el libro The Joy of π, página 71. Allí aparece también las siguientes citas:
|
|
E = mc2
|
Pocas fórmulas hay tan famosas como esta. Ni tan influyentes. Obtenida por Albert Einstein hace ahora cien años (como pasa el tiempo), es por un lado el símbolo del ataque y derribo de la mecánica newtoniana que supuso la teoría de la relatividad. Por otro, es la receta de la fuente de energía más potente y devastadora de cuantas hemos desarrollado hasta ahora: la energía nuclear. Su significado físico queda más patente si elegimos las unidades de modo que la velocidad de la luz sea 1, es decir, una unidad de espacio por unidad de tiempo. En tales circunstancias, la fórmula se simplifica y queda: E = m, es decir, que la energía y la masa son equivalentes. Casi nada. |
 |
Tenemos el número e, trascendente; el número π, también trascendente; y la raíz cuadrada de 163, que es irracional. Sin embargo, el resultado está extraordinariamente cerca de un número entero. Otro hallazgo de Ramanujan.
The number sense, p.149. |
|
13+23+33+...+n3 = (1+2+3+...+n)2 |
Luis Gómez (16-7-2003) manda la siguiente identidad: 100=1³+2³+3³+4³. Se trata de un caso particular de la estupenda fórmula que se ve a la izquierda, y que expresada mediante sumatorios es: Se demuestra fácilmente por inducción y se debe a Nicomaco, que la dedujo de la fórmula de Pitágoras acerca de la suma de los n primeros impares y de la siguiente observación:
Boyer, p.237. |
|
v - a + c = 2 |
En todo poliedro convexo, el número de vértices menos el número de aristas más el número de caras es igual a dos. Esta fórmula, debida a Euler, muestra un invariante algebraico asociado a un espacio topológico (lo cual quiere decir que se mantiene bajo deformaciones continuas del objeto) y tiene como consecuencia fundamental el que solo haya cinco poliedros regulares. Además, la simetría entre V y C da lugar a los dualismos entre los poliedros: cubo-octaedro, dodecaedro-icosaedro, y tetraedro-tetraedro. Algunos la sitúan en el inicio de la topología. Eso sí: bonita, lo que se dice bonita, no es. |
 |
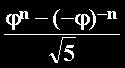Esta fórmula, atribuida a Édouard Lucas, es uno de esos extraordinarios ejemplos en los que objetos matemáticos que en apariencia nada tienen que ver entran en relación: a la izquierda se puede ver el término general de la sucesión de Fibonacci, es decir, la fórmula que proporciona para cada número natural n el término enésimo de la sucesión. Hasta aquí no hay nada raro. Lo sorprendente es que la letra φ que aparece por dos veces representa, naturalmente, la sección áurea. Casi nada. Mathematical Recreations and Essays, p.57. Allí la fórmula aparece igual que aquí, pero con la letra τ en vez de con la letra φ. |
 |
Ha sido al escribir la reseña de la película 2001 y hablar de las dimensiones del monolito cuando he recordado esta fórmula. Podría haberla escrito igualmente
Esta expresión, debida a Pitágoras, se visualiza fácilmente de la siguiente manera: Empezando por el círculo de arriba a la izquierda y añadiendo gnomones se ve como al añadir cantidades impares la cantidad total de círculos siempre es un cuadrado perfecto. |
|
c2 = a2 + b2
|
Sí, efectivamente: es él, el teorema de Pitágoras: "en todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos". El teorema ya era conocido por los babilonios de la época de Hammurabi más de mil años antes de que los griegos le diesen nombre, y lo utilizaron para obtener lo que hoy conocemos como ternas pitagóricas, por ejemplo (3,4,5) o (5,12,13), que son ternas de números naturales que cumplen el teorema. Si fueron los babilónicos los primeros en descubrir el teorema, ¿por qué lleva el nombre de Pitágoras? Bueno, parece ser que los pitagóricos en lo que sí fueron los primeros fue en demostrar el teorema, cosa que puso tan contento a Pitágoras que, según la leyenda, sacrificó cien bueyes (es decir, realizó una hecatombe) en agradecimiento a los dioses (los pitagóricos eran un poco raros). Struik, pp.26, 28, 42. |
 |
La sección áurea es solución de la ecuación Si despejamos el término cuadrático y tomamos raíces cuadradas tenemos: Si ahora sustituimos la φ del radicando por su valor, que es la raíz completa, y repetimos el proceso indefinidamente, obtendremos la fórmula de la izquierda. ¿Te ha gustado? Pues te aconsejo que veas φ como fracción continua. |
 |
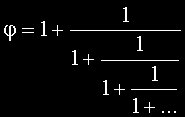La sección áurea es solución de la ecuación El término cuadrático se puede considerar como un producto, Si ahora sustituimos la φ del denominador por su valor, que es la suma, y repetimos el proceso indefinidamente, obtendremos la fracción continua que puedes ver. ¿Te ha gustado? Pues te aconsejo que veas φ como raíz infinita. |
 |
Que el irracional y trascendente valor del número π se pueda calcular echando mano únicamente del dos y de productos, divisiones y raíces cuadradas ya resulta sorprendente. Pero lo más destacable de esta fórmula, debida al matemático francés François Viète, es que en ella, por primera vez, un proceso infinito, simbolizado por esos tres puntos que se ven a la derecha, se indicaba explícitamente en una fórmula matemática. Lo que realmente obtuvo Viète fue siendo lo que se ve a la izquierda la forma numérica de lo anterior tras escribir el valor del coseno de pi cuartos y aplicar la fórmula del coseno del ángulo mitad. Pregunta: ¿cuál de las dos fórmulas crees más informativa? |
 |
Normalmente la belleza matemática estriba en la simplicidad y la simetría con las que los elementos se relacionan. Sin embargo, esta fórmula me atrae como me atraen a veces algunas piezas barrocas por justo lo contrario: surgida, creo, de la mente del matemático hindú Srinivasa Ramanujan, es tal la profusión de cifras y signos que la expresión parece vibrar como si fuese una colonia de insectos. Me pregunto: ¿de dónde sacó Ramanujan algo así? |
 |
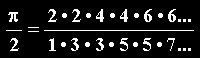Hay muchas formas de obtener π mediante procesos infinitos. Una de mis preferidas es la fórmula de la izquierda, debida al matemático John Wallis. La obtuvo en 1655 como resultado de su búsqueda del área del círculo. Lo que más llama la atención en ella es su tremenda sencillez: utilizando únicamente números naturales, productos y cocientes obtenemos el irracional y escurridizo número π. |
 |
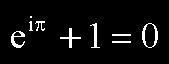¿No es increíble la fórmula de Euler? No es de extrañar que en cierta ocasión el matemático Benjamin Peirce les dijese a sus alumnos: "Caballeros, esto es sin duda cierto, es absolutamente paradójico, no podemos comprenderlo y no sabemos lo que significa, pero lo hemos demostrado y, por lo tanto, sabemos que debe ser verdad". En realidad, Euler dijo mucho más con sus famosas identidades, siendo la fórmula de la izquierda el caso particular x = π:
|
.
,
pero he preferido dejarla desarrollada para que no se pasase por alto
el hecho de que estamos sumando números impares y que estos resultan
ser los saltos que hay que dar para pasar de un cuadrado a otro:
.
. 
, y después despejar φ. Resultado: 
. 
,