Conteo
1. Un turista debe trasladarse de una ciudad a otra. Para hacerlo puede optar por viajar en aviÃģn, camiÃģn Ãģ tren. Y en cada uno de estos transportes puede elegir en primera o en clase turista. ÂŋDe cuÃĄntas maneras distintas puede realizar el viaje?
2. Ahora nuestro turista decide visitar 5 ciudades en determinado orden. Para cada traslado tiene las mismas opciones que antes. ÂŋDe cuÃĄntas formas puede realizar su recorrido?
3. En una fiesta se encuentran 10 hombres y ocho mujeres. ÂŋDe cuÃĄntas formas pueden integrarse en parejas para bailar una pieza?
4. ÂŋCuÃĄntos mÚltiplos de 3 hay entre 10 y 226?
5. ÂŋCuÃĄntos son los nÚmeros naturales tales que ningÚn dÃgito es 1 y el producto de todos sus dÃgitos es igual a 48?
| 6. ÂŋDe cuantas maneras se puede colorear el siguiente mapa, utilizando a lo sumo 4 colores con la condiciÃģn de que los estados limÃtrofes tengan colores diferentes? |
 |
| 7. ÂŋCuÃĄntos cuadrados hay en el dibujo? |
 |
8. Con cuatro unos y cuatro nueves se desea construir un nÚmero de 8 cifras que sea divisible entre 11. ÂŋDe cuÃĄntas maneras puede hacerse?
9. ÂŋCuÃĄntos nÚmeros menores que 13000 son tales que el producto de sus dÃgitos es 30?
10. Todas las calles de un pueblo son rectas, sin que haya dos paralelas. Al emplazar un farol en cada cruce se colocaron en total 66 faroles. ÂŋCuÃĄntas calles tiene el pueblo como mÃnimo?
11. ÂŋDe cuÃĄntas maneras se pueden elegir tres nÚmeros enteros distintos, entre los nÚmeros del uno al quince, de modo que su suma sea un mÚltiplo de 3? (El orden no importa).
12. Juntamos 1000 cubos de lado 1 para formar un cubo de lado 10. Lo pintamos y luego lo descomponemos en los cubos originales. ÂŋCuÃĄntos de los cubos tienen al menos una cara pintada? ÂŋCuÃĄntos de los cubos tienen solo una cara pintada? ÂŋCuÃĄntos de los cubos tienen al menos dos caras pintadas?
13. El alfabeto de unos extraterrestres estÃĄ compuesto por 6 letras: *, §, **, §§, *§, §*. Ana encontrÃģ escrita una palabra, pero sin separaciÃģn entre una letra y otra: *§§** §*. ÂŋDe cuÃĄntas maneras se puede leer la palabra?
14. Se trazan 43 rectas en el plano concurrentes en un punto O. Ahora trazamos una recta que no pasa por O y que no es paralela a ninguna de las 43 anteriores. ÂŋEn cuÃĄntas regiones queda dividido el plano.
15. Mirena, Marcela y Juliana se reparten 10 balones. A cada una le toca por lo menos uno. ÂŋDe cuÃĄntas maneras distintas pueden hacer el reparto? ÂŋSi se repartieran 100 balones?
16. Tenemos un tablero cuadriculado de 100 à 100. Las filas fueron numeradas de 1 a 100, de arriba hacia abajo. Del mismo modo, las columnas fueron numeradas de 1 a 100, de izquierda a derecha. A continuaciÃģn, en cada columna, se pintaron las casillas que estÃĄn en las filas cuyo nÚmero es un divisor del nÚmero de la columna. (Por ejemplo, en la columna 12, se pintaron las casillas de las filas 1, 2, 3, 4, 6 y 12; en la columna 13, se pintaron las casillas de las filas 1 y 13). a)Determina el nÚmero de casillas que se pintaron en la sÃĐptima fila.. b) Determina el nÚmero de casillas que se pintaron en todo el tablero.
17. En un hospital, a cada reciÃĐn nacido se le coloca una pulsera formada por cinco cuadritos con dÃgito escrito en cada uno de ellos. ÂŋCuÃĄntas pulseras distintas puede haber?
Nota: La pulsera 2 - 0 - 3 - 4 - 5 es la misma que la pulsera 0 - 3 - 4 - 5 - 2 sÃģlo que girada.
18. Se tienen dos rectas paralelas. En una de ellas hay marcados 6 puntos y en la otra 4 puntos. Cada uno de los 6 puntos de la primera recta se une por medio de un segmento con cada uno de los 4 puntos de la segunda recta. Hallar cuÃĄntas veces se cruzan todos los segmentos que unen los puntos, sabiendo que en ningÚn punto se cruzan mÃĄs de dos segmentos.
Nota: no se cuentan los 10 puntos que estÃĄn sobre las rectas originales.
19. Con los dÃgitos 1, 2, ... , 9 ÂŋcuÃĄntos nÚmeros de tres cifras distintas se pueden formar con la condiciÃģn de que la suma de sus cifras sea par?
20. En un octÃĄgono regular se dibujan los triÃĄngulos isÃģsceles que tienen por vÃĐrtices tres vÃĐrtices del octÃĄgono.
a) ÂŋCuÃĄntos son?
b) Se pintan tres vÃĐrtices cualesquiera del octÃĄgono rojo y los otros cinco de azul.
Para cada forma de pintar los vÃĐrtices, ÂŋcuÃĄntos triÃĄngulos isÃģsceles tienen los tres
vÃĐrtices del mismo color?
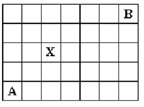
| 21. En la cuadrÃcula de la figura, Âŋde cuÃĄntas maneras podemos ir de la casilla A a la casilla B, moviÃĐndose siempre o bien una casilla hacia la derecha o bien una casilla hacia arriba? ÂŋDe cuÃĄntas maneras, si debemos pasar por la casilla X? |
 |