Geometría
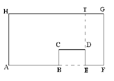
| 1. El rectángulo AFGH tiene 60 cm de perímetro y el rectángulo BCDE tiene 24 cm de perímetro. La longitud de BE es de 8 cm y la de DT es de 10 cm. Encontrar el área de la figura ABCDEFGH. |
 |
2. ¿Cuántos triángulos distintos hay de perímetro 17 y lados enteros?
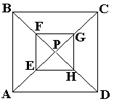
| 3. ABCD es un cuadrado. E, F, G y H son los puntos medios de AP, BP, CP y DP respectivamente. ¿Cuál es la razón de las áreas del cuadrado EFGH y el cuadrado ABCD? |
 |
4. Determinar los valores enteros de x tales que el triángulo de lados 5, 8 y x es obtusángulo.
| 5. El rectángulo ABCD tiene 3 m de largo por 2 m de ancho. Se corta la diagonal AC con los puntos E y F en tres segmentos iguales. ¿Cuál es el área del triángulo BEC? |
 |
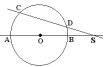
| 6. En la figura, AB pasa por el centro de la circunferencia O y corta a la secante CD en el punto S (un punto exterior al círculo) tal que DS es igual a CO, el radio del círculo. Si el ángulo AOC mide 57° ¿, ¿cuánto mide el ángulo DSB? |
 |
7. Para dividir un pastel entre 16 invitados se corta en el centro una porción circular de 3 cm. de radio y el resto se divide en 15 porciones iguales, que resultan del mismo tamaño que la porción central. Si quisiéramos dividir el mismo pastel y con el mismo procedimiento entre 25 invitados, ¿cuál debería ser el radio de la porción central?
| 8. La figura de la derecha está formada por 6 cuadrados. ¿Cuánto mide el ángulo CBA? |
 |
9. El lado de un triángulo equilátero es 3/7 del lado de un cuadrado. ¿Cuál es la razón de sus perímetros?
10. Los tres vértices de un triángulo están en un círculo cuya área es pi. Dos de los vértices están en un diámetro. ¿Cuál es el máximo valor que puede tener el área del triángulo?
11. Un triángulo equilátero y un hexágono regular tienen el mismo perímetro. ¿Cuál es la razón de sus áreas?
12. En un trapecio rectangular de 240 cm² de área y 12 cm de altura, la diferencia entre la base mayor y la base menor es de 9 cm. ¿Cuál es el perímetro del trapecio?
13. En el triángulo ABC se trazan las bisectrices de los ángulos B y C que se cortan en P. Por P se traza una paralela a BC que corta al lado AB en D y al lado AC en E. Se sabe que BD = 5.3 y CE = 7.8. Calcular la medida del segmento DE:
| 14. De una hoja rectangular se quiere cortar una figura formada por un semicírculo y un triángulo, como se ve en la figura. ¿Cuál es el área del papel desperdiciado? |
 |
15. Sean C1 y C2 dos circunferencias concéntricas y C 3 una circunferencia exterior a C 1, interior a C 2 y tangente a ambas. Si el radio de C 2 vale 1, ¿cuánto debe valer el radio de C 1 para que la superficie de C 1 sea el doble que la de C3?
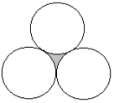
| 16. En la figura de la derecha, formada por tres círculos de 1 cm de diámetro y tangentes entre sí, calcular el área de la zona sombreada. |
 |
17. Sea ABC un triángulo tal que el ángulo B + el ángulo C = 5 el ángulo A. Si O es el punto de intersección de las bisectrices de el ángulo A, el ángulo B y el ángulo C, calcular la medida del ángulo BOC.
18. En el triángulo ABC, el ángulo A = 27º y el ángulo B =42º . Sobre el lado AB se marca el punto D de modo tal que el ángulo ACD=69º y sobre el lado AC se marca el punto K tal que DK sea paralela a BC. Calcular las medidas de los ángulos CBK y ABK.
|
19. En la figura E, F, G y H son los puntos medios de los lados
del cuadrado ABC a) ¿Cuál es la razón del área del
triángulo BGC y el área del cuadrado grande? |
|
20. En el cuadrilátero ABCD el ángulo A mide 42º . Se traza la diagonal BD y resulta que el ángulo ABD es el doble del ángulo exterior a B y el ángulo BDA es el doble del ángulo exterior a D. ¿Cuánto mide el ángulo C?
21. Sea ABC un triángulo tal que el ángulo A = 56º y el ángulo B = 65º . Se traza por cada vértice la bisectriz exterior y queda determinado un nuevo triángulo PQR. Hallar el ángulo P, el ángulo Q y el ángulo R.
| 22. A es centro de la circunferencia I. B es centro de la circunferencia II y es un punto de la circunferencia I. El diámetro CD de la circunferencia I = mide 4 u. Calcular el área rayada en la figura de la derecha | 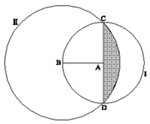 |
23. Sea ABC un triángulo y P, Q y R los puntos medios de sus
lados. Demuestra que el perímetro del triángulo formado
por P, Q y R es la mitad del perímetro de ABC.
| 24. En una circunferencia, dos cuerdas perpendiculares AB y CD se cortan en un punto E, como se indica en la figura. Hallar la longitud de la circunferencia |
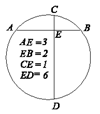 |
| 25. ABCD es un cuadrado de 4 cm de lado, E y F son puntos medios de los lados. BE es un arco de circunferencia de radio de igual longitud que BE. ¿Cuál es el área de la figura sombreada? |
 |
| 26. En el trapecio ABCD se han trazado las diagonales y dos rectas paralelas entre sí, una por C y la otra por D, como se muestra en la figura. Demostrar a = b + c + d. |
 |
| 27. Por un punto P en el interior del triángulo rectángulo ABC se trazan segmentos paralelos a los lados del triángulo. Si las áreas de los tres triángulos que se forman, como se indica en la figura, son 2, 8 y 18, hallar el área del triángulo ABC. |  |
28. Demuestra que los ángulos opuestos de un cuadrilátero inscrito en una circunferencia son suplementarios.
| 29. ABCD es un cuadrado inscrito en una circunferencia. Demuestra que PC y PD trisecan al ángulo APB. |
 |
30. Dos triángulos isósceles cuyos lados miden x,x,a
y x,x,b respectivamente, tienen igual área; a
es desigual b.
Hallar x.
| 31. P, Q, R y S son puntos de tangencia. Demuestra que AB + DC = AD + BC |
 |
| 32. En un pentágono regular ABCDE, trazamos las diagonales AC y BE, que se cortan en el punto P. Recortamos el triángulo APB y obtenemos así el hexágono APBCDE. Tenemos una colección infinita de piezas iguales en tamaño y forma al hexágono APBCDE. Muestra que se puede teselar (Teselar o embaldosar el plano significa cubrir cualquier extensión plana colocando piezas juntas, sin que queden huecos entre ellas.) el plano con estas piezas. |
 |